Python 素数を詰めるナップサック

概要

なんか最近、ナップサックにモノを詰めてばっかじゃねーか……? しかも今回詰めるのは……素数……。というわけでやってまいりました、 Python の時間です。

今回のプログラミング問題はこちら。

• N が 1〜20000 で与えられます。
• 2〜N までに含まれる素数を出してください。
• ほんでその素数リストから好きなだけ素数を取り出してください。
• その和が N ぴったりになる組み合わせの中で、最大個数を出せ!
• そもそも N ぴったりなんて作れねえ! ってときは -1 を出せ!

ほぎゃー! ナップサック・シリーズ最終回! 素数ナップサックのスタートだ!

考え方

• N までの素数リストの出し方は昔ガンバって作ったので流用する。
  • (2017-12-08)Python 素数
• リストの要素の重さと価値を決める。
  • フツーのナップサック問題では品にはそれぞれ (weight, value) がある。
  • 今回はリストの内容が品物ではなく素数なので、何が価値で何が重さなのかわかりづらいが、素数においては重さが素数の数値で、価値はすべて 1 だ。だって「最大個数」が「最大価値」であるから、各々の価値は同じだからだ。
• dp 表を作る。
  • フツーのナップサック問題では「リストから 0〜全部 選べるとき」「重さ制限が 0〜N のとき」のふたつの軸をもつ表に「その条件での価値最大値」を埋めていって、一番最後のマス「全部選べるとき」「重さ制限が N のとき」の「価値最大値」を求めた。
  • しかし今回は「素数リストから 0〜全部 選べるとき」「重さが 0〜N ぴったりのとき」のふたつの軸をもつ表を埋めていって、一番最後のマス「素数全部選べるとき」「重さが N ぴったりのとき」の「価値最大値」を求める。
• 重さぴったり 0 を作るには、リストから何も選ばないのが正解なので 0 行目は全部 0 になる。
• リストから 0 個選べるときに 1〜N を作ることはできないので、 0 行目以外の 0 列目は -1 にしておく。以降、 -1 は「不可」を表す。 None のほうが見た目わかりやすいんだけど、マス同士を比較するときイチイチ数値に直さないといけなくなるから最初から数値にしとくよ。
  • あと問題に不可のときは -1 ってのもあるから、一石二鳥だ。
• マスは左から埋めていく。
  • すでに埋まっているマスが、「不可」だったら計算する意味がないのでスキップ。
  • n 個で作れるときは、次の素数を足すと、合算値としてはそのマスから次の素数ぶん下に移動したところの重さになるから、そこんとこのマスに n + 1 を格納する。モチロン、格納するのはその重さの現段階での最大値を上回っているときだけだ。

なげーぞ。クソックソッ、考える過程で自分が陥ったミスや勘違いを防ごうと説明を足すほど理解を難しくしている気がしてくるぜ!

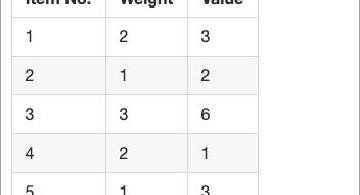
N = 18 だったら素数リストは [2, 3, 5, 7, 11, 13, 17]

→横: 素数リストから選べる個数
↓縦: この重量をぴったり作れるとき、という条件

|     | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0   |   |   |   |   |   |   |   |   |
| 1   |   |   |   |   |   |   |   |   |
| 2   |   |   |   |   |   |   |   |   |
| 3   |   |   |   |   |   |   |   |   |
| ... |   |   |   |   |   |   |   |   |
| 18  |   |   |   |   |   |   |   |   |

各マスには「* 個選べて」「重さの和が * ジャストになる」ときの「価値最大値」が入る。

最初からワカってるところを埋める。 -1 は「この重さは作れない」を表す。

|     | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0   | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1   |-1 |   |   |   |   |   |   |   |
| 2   |-1 |   |   |   |   |   |   |   |
| 3   |-1 |   |   |   |   |   |   |   |
| ... |   |   |   |   |   |   |   |   |
| 18  |-1 |   |   |   |   |   |   |   |

「作れる」マスに次の数を足して、

|     | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0   | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1   |-1 |   |   |   |   |   |   |   |
| 2   |-1 | 1 |   |   |   |   |   |   |
| 3   |-1 |   |   |   |   |   |   |   |
| ... |   |   |   |   |   |   |   |   |
| 18  |-1 |   |   |   |   |   |   |   |
            ↑重さ 0 に素数ひとつめの 2 を足したので重さは 2 のマスに入れる。
              素数ひとつの価値は 1 なので、もともとの 0 に + 1 した値を入れる。

Python さん出番です

方針が決まったらスクリプトを書き起こすぞ!

from pprint import pprint
from math import sqrt


def prime(N: int):
    """問題を解きます。"""

    # 素数一覧。
    primes = get_primes_until_n(N)
    # pprint(primes)

    # 表を作る。
    # 列の数は、 len(primes) + 1。選ばない(= 0)ときの行があるからひとつ多い。
    # 行の数は、 N + 1。重量 0 のときの行があるからひとつ多い。
    # NOTE: -1 は、「その重さは作れない」ことを意味します。
    # NOTE: メモリ効率のためリストオブジェクトは繰り返し使います。
    _ = [0] + [-1] * N
    dp = [_ * 1 for i in range(len(primes) + 1)]

    # 列を埋めていきます。
    for i in range(len(primes)):

        # i の周回では primes[i] まで選べるときの計算をします。
        # NOTE: 表でいえば i+1 列目ね。
        value = 1
        weight = primes[i]

        # 行を埋めていきます。
        for w in range(N + 1):

            # 現在のマスに素数を足した場合を検証します。
            # が、今は「作れない」マスならスキップ。
            # 足して N を超えるなら問題外なのでこれもスキップ。
            if dp[i][w] != -1 and w + weight <= N:
                dp[i + 1][w + weight] = dp[i][w] + value

            # あとひとつ右のマスも更新しておきます。
            dp[i + 1][w] = max(dp[i][w], dp[i + 1][w])

    # dp テーブル作り終わりました。
    # この表には、素数が i 個選べるとき w をぴったり作れる素数の最大個数が入っています。
    pprint(dp)
    # 一番右下の数が、「素数リストから好きなだけ選んで」「N をぴったり作れる」素数の最大個数です。
    return dp[-1][-1]


def get_primes_until_n(N: int):
    """N までの素数一覧を返します。"""

    # 2〜N の dictionary です。
    # この先の処理で、素数でないものは False にしていきます。最終的に値が True のまま残った key が素数です。
    # NOTE: list にして、 index を key 扱いしたほうがイカすんだけど dictionary のほうがわかりやすいかと思って。
    dic = {i: True for i in range(2, N + 1)}

    # N の平方根までチェックすれば、全部の数の素数判定は終わります。
    for i in range(2, int(sqrt(N)) + 1):

        # すでに False(素数ではない)判定になっているものは計算不要です。
        if dic[i] is False:
            continue

        # 2 から始まるので、その先の倍数を全部 False(素数ではない)にしていけば最後には素数だけが True で残ります。
        j = i * 2
        while j <= N:
            dic[j] = False
            j += i

    return [i for i in dic.keys() if dic[i]]


print(prime(18) == 3)

[[0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
 [0, -1, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
 [0, -1, 1, 1, -1, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
 [0, -1, 1, 1, -1, 2, -1, 2, 2, -1, 3, -1, -1, -1, -1, -1, -1, -1, -1],
 [0, -1, 1, 1, -1, 2, -1, 2, 2, 2, 3, -1, 3, -1, 3, 3, -1, 4, -1],
 [0, -1, 1, 1, -1, 2, -1, 2, 2, 2, 3, 1, 3, 2, 3, 3, 3, 4, 3],
 [0, -1, 1, 1, -1, 2, -1, 2, 2, 2, 3, 1, 3, 2, 3, 3, 3, 4, 3],
 [0, -1, 1, 1, -1, 2, -1, 2, 2, 2, 3, 1, 3, 2, 3, 3, 3, 4, 3]]
True

設計した表と pprint したときの表示では縦横方向があべこべだからちと見づらいが、
ようは↑で作った dp 表は↓の表をあらわしている。

|     | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0   | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1   |-1 |-1 |-1 |-1 |-1 |-1 |-1 |-1 |
| 2   |-1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3   |-1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| ... |   |   |   |   |   |   |   |   |
| 17  |-1 |-1 |-1 |-1 | 4 | 4 | 4 | 4 |
| 18  |-1 |-1 |-1 |-1 |-1 | 3 | 3 | 3 |

完成だ!

おしまい

というわけで、とうとう素数までナップサックに詰めたところで、ナップサック遊びはおしまいだ。オリジナルのナップサックでは、「品物を入れるときはナップサックにその品が入るだけのスペースをあけなければならない」ことを理解するのが最後のカベだったけれど、今回は「埋まらないマスもある。なぜならその重量を作れないパターンもあるのだから」というところが最後のカベだったな。

そう、 0 じゃねーのだ。作れないのだから。