緑さんでも分かるナップサック問題解説アルゴリズム編

概要
ナップサック問題ってなに
動的計画法練習編
動的計画法本番
緑さんでも分かる解説終わり
Omake

概要

ナップサック問題を自分なりに理解したので書く。いやあ、一年前に取り組んだ、停止性問題を思い出すぜ! 理解に一週間以上要したところとかな!

(2019-03-06)停止性問題を自分なりに理解する

この問題の説明はたくさんネットにあるのだけど、そのほとんどでぼくがよく理解できなかった。なので今回は、既存の情報の中で緑さんがつまずいたところをしっかりおさえた、自分なりの攻略記事を書くぞ。

ナップサック問題ってなに

「ナップサックの中にどんだけ効率よく品物を詰められるか?」っていう問題だ。

品物には、それぞれ「重さ」と「価値」がある。当然だな。
ナップサックには重量制限があって、決められた重量以上に品物は詰められない。当然だな。
さあ! なるべく「価値」の合計値がたくさんになるように品物を詰めろ!

こんなもんカンタンだぜ、品物の全組み合わせを算出して、全部の合計を算出すればいいだろうが!

いや、これでイケそうなんだが、さて、組み合わせとやらは一体何通りあるんだってハナシになるわけだ。ちっと計算してみたが、ざっとこんな感じになる。(計算プログラムは下に載せておく。)

1個あるとき……1
2個あるとき……3
3個あるとき……7
4個あるとき……15
5個あるとき……31
6個あるとき……63
7個あるとき……127
8個あるとき……255
9個あるとき……511
10個あるとき……1023
11個あるとき……2047
12個あるとき……4095
13個あるとき……8191
14個あるとき……16383
15個あるとき……32767
16個あるとき……65535
17個あるとき……131071
18個あるとき……262143
19個あるとき……524287
20個あるとき……1048575
21個あるとき……2097151
22個あるとき……4194303
23個あるとき……8388607
24個あるとき……16777215
25個あるとき……33554431

25品目のとき、三千万通りだと……? これで良いなら良いのだけれど、これだと品物が増えたとき膨大な時間がかかってしまう。(こういうプログラミング問題を解こうと思ったのがことの発端なんだけど、そのとき最初に作ったプログラムでは、一時間経っても処理が終わらなかった。サイテーだ。)だから、もっと効率的な方法はないのか? と考えるのがナップサック問題だ!

ナップサックにモノをぎゅうぎゅう詰めていく、っていうポップなイメージなのが良いよね。

動的計画法練習編

「もっと効率的な方法」が、動的計画法っていうアルゴリズムなんだが、いきなりこの方法でナップサックに取り組むと混乱するんだ。だからもっと簡単な例で、まずは動的計画法に慣れる。

「数値をいくつか用意したから、その中から好きなだけ数値を選んで、合計が最大になるものを出せ!」という問題だ。

たとえば [7, -6, 9] なら最大の組み合わせは 7, 9 で最大値は 16 だ。
たとえば [-9, -16] なら何も選ばないのが答えで、最大値は 0 だ。

もちろんこの問題で一番良いのは、「正の数だけ出して全部足す」という方法だ。だけどこれをあえて動的計画法で解く。今回の記事は「緑さんでも分かる」であるから、ぼくが一番理解しやすかった道筋でいくぜ。

まず表↓を用意する。列番号は、「リストから何個目まで数字を選ぶか」という番号を表す。

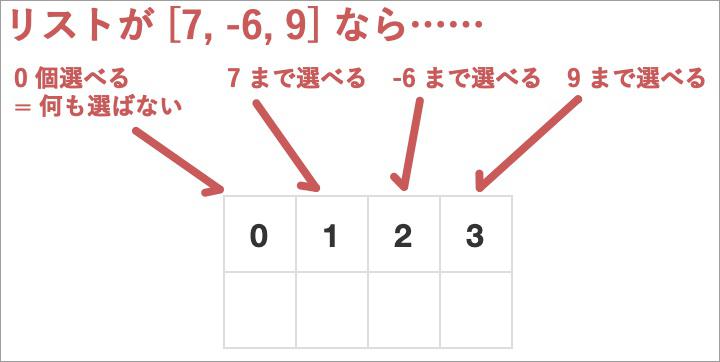
そして列番号の下には、その条件下での合計最大値を入れていくのだ。

0 個選べるときは当然最大値は 0 だ。
7 まで選べるなら、もちろん 7 だろう。
列番号 1 のとこに「リストの最初の数まで選べるときの最大値」が入るのなら、いちばん右は「リストから全部選べるときの最大値」が入ることになる。それはすなわち、この問題の答えだ。

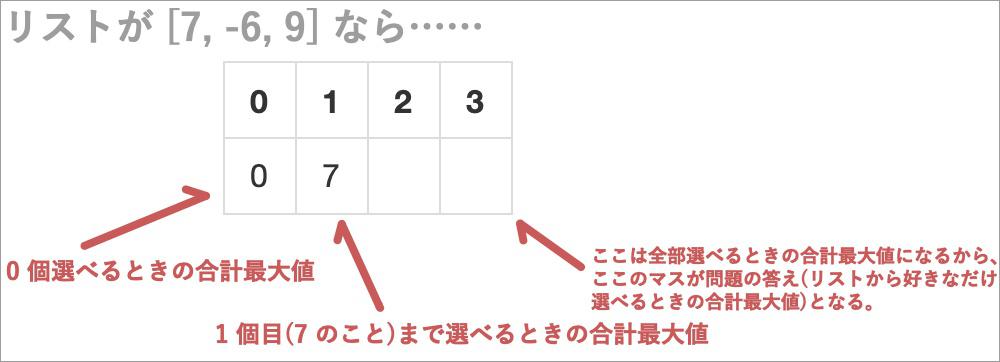
画像↑に続けて列番号 2 にも数値を入れるときは、とりあえずひとつ前の数字に足してみる。そうすると 7 - 1 = 1 になる。現在のところの最大値は 7 だから、これはどうやら、リスト 2 つめの数は足さないほうがよいみたいだとわかる。 1 つ目の数まで選べるときの最大値と、 2 つ目までの数を選べるときの最大値は同じだから、そのようにマス目を埋める。

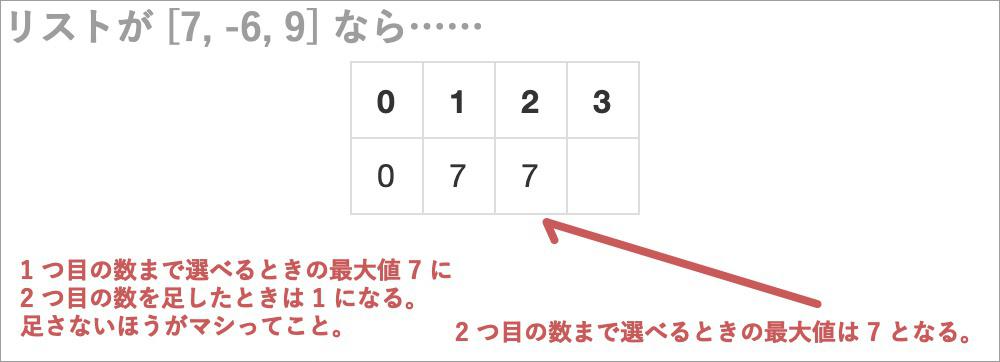
続けて列番号 3 にも数値を入れる。

「数字が 3 つはいっているリストから 3 つ選べるときの合計最大値」というのは、問題である「リストから好きなだけ選んで合計最大値を作れ」の答えである。これで完了だ。

ぶっちゃけ今回の問題では表を作る必要なんてなくて、ただ「現在のところの最大値」だけをメモしておいて、更新があればそれを書き換えていけば済む。けれどこれはナップサック問題のための練習だから。
表を作るとき、列番号が何を意味するのか、マス目の数字が何を意味するのかをハッキリさせるのが大事だと思う。
今回ならば、列番号は「* 個目までの数字を選べるとき」という条件を表す。マス目は「その条件での数値合計最大値」を表す。

動的計画法本番

上述の例のように、条件が低いところから順々に条件を増やして計算していく方法で、冒頭のナップサックへ品物を詰めていくぞ。今回の例では、条件は次のとおりとする。

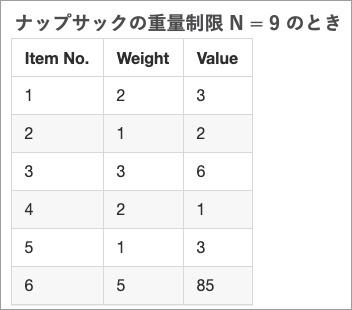
まずは表を作る。詰められる品物は 6 個だ。

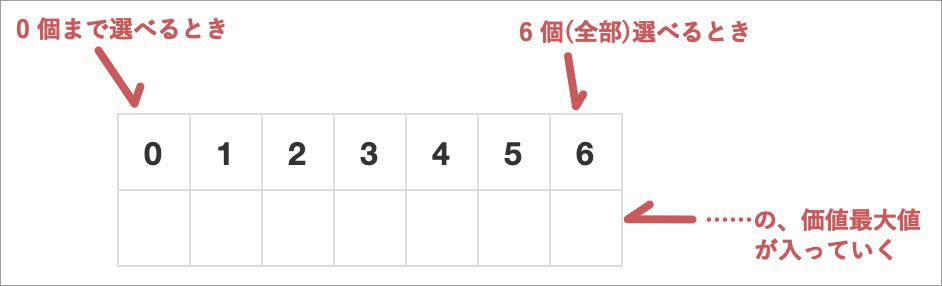
練習編では、ただ単純に「最大は大きければ大きいほどよい」だった。けど今回は、「最大は 9 を超えてはいけない」という制限がある。だから、列で「個数制限 0〜max」を表現したように、行で「重量制限 0〜制限値」を表現する。そのどちらも、 0 から段々増やして、「ひとつ前」と比べていけば良いってわけだ。

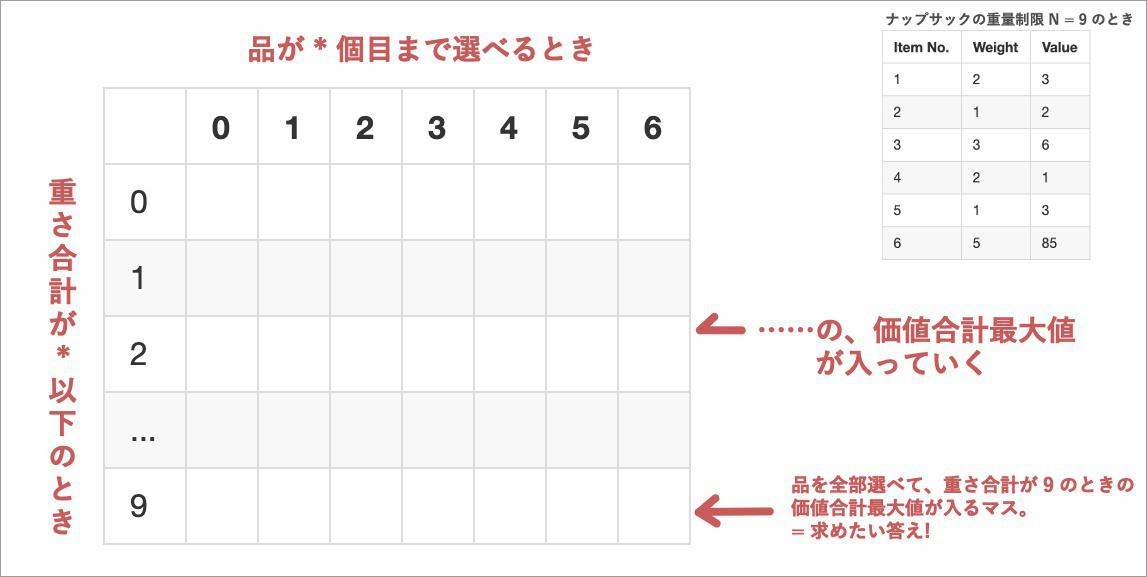
ではマスを埋めていこうや。

品が 0 個目まで選べるときの最大値ってゼロしかなくね?
重さ制限が 0 のときって何も品が詰められないのだからゼロしかなくね?

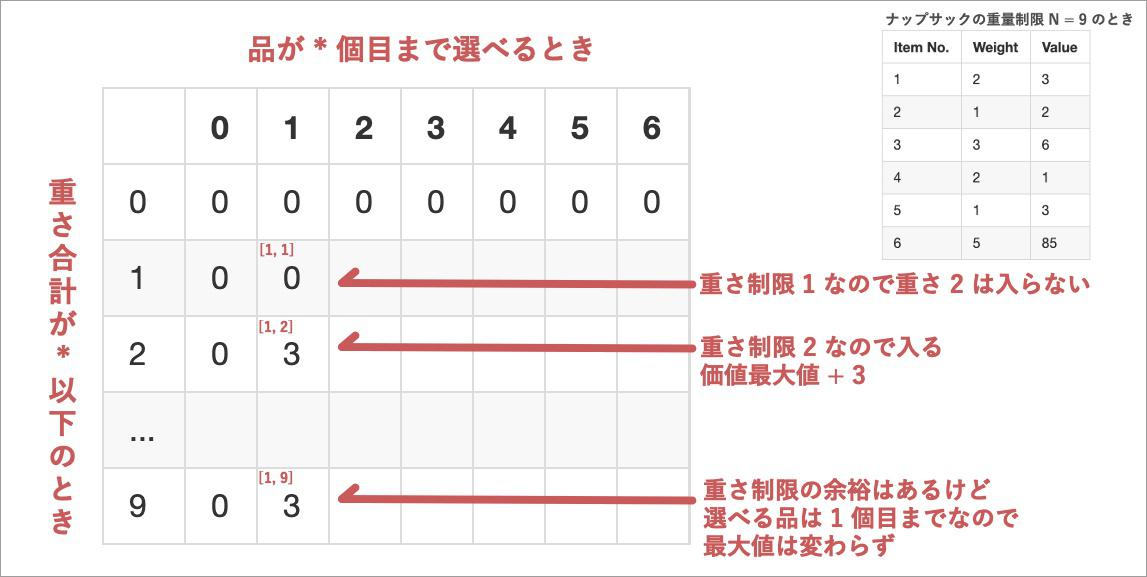
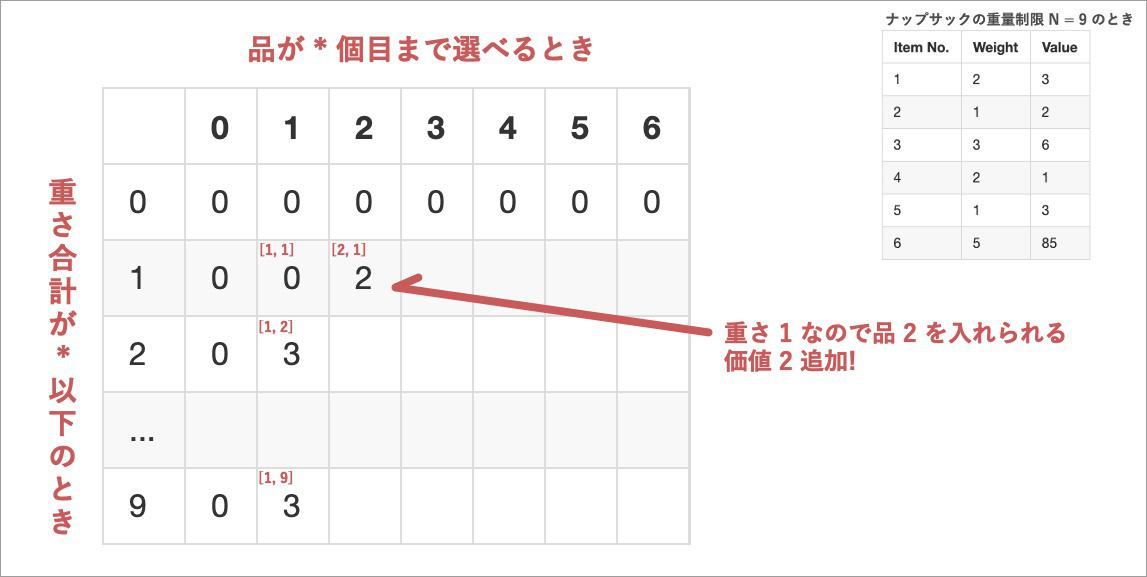
[1, 1] のマスには「1 個目の品まで選べて、重さ制限 1 のときの最大価値」が入る。 1 個目の品は (weight, value) = (2, 3) だから、重さ制限 1 のマスには入れない。スキップだ。
[1, 2] のマスは重さ制限 2 だから、品 1 は入ることができる。入れよう。価値は 3 だから 3 を入れる。
そのまま下に続けていき [1, 9] のマスだ。どんだけ重さ制限がゆるくなっても、入れられる品は 1 個目だけっていう列だから、最大価値は 3 だ。

[2, 1] のマスでは品 2 まで選べる。重さ制限は 1 で品 2 は (weight, value) = (1, 2) なので入れることができる。
重さ制限 1 では品 1 は選べなかった。今の所重さ制限 1 のときの最大価値(ひとつ左のマス)は 0 だ。まあこれは入れちゃっていいだろう。品 2 の価値である 2 を入れる。

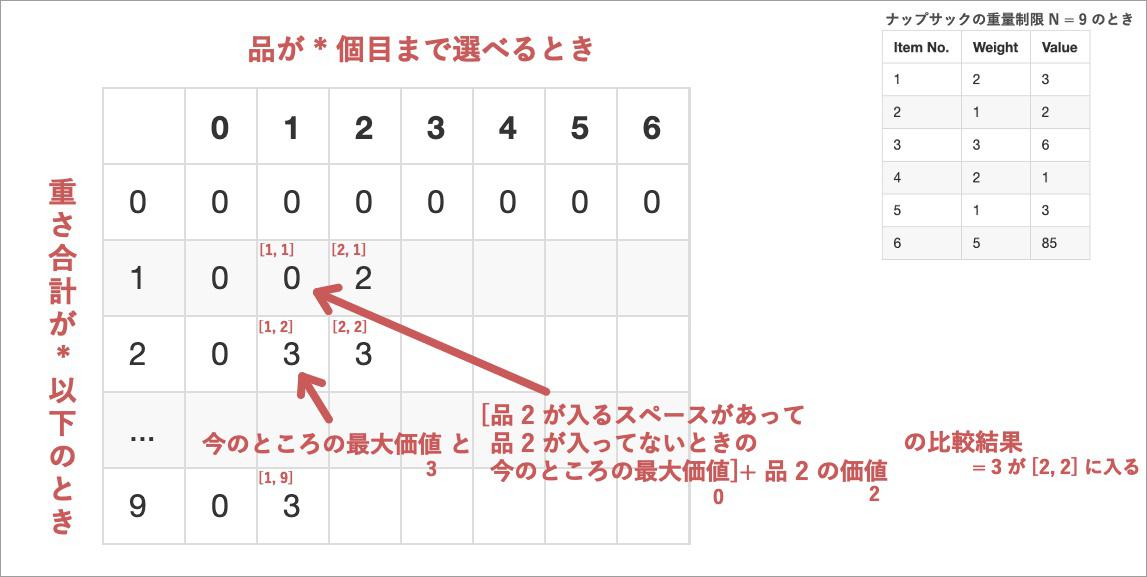
[2, 2] はひとつ重さ制限がゆるくなっているから、もちろん品 2 を入れることができる。
ただ重さ制限が 2 のときだから、品 1 がすでに入っていたはずだ。品 1 まで選べる条件での最大価値と、品 2 を足した場合の価値を比べよう。
品 1 まで選べる条件での最大価値は、ひとつ左のマスにある。
品 2 を足すということは、品 2 ぶんの重さの余裕がないといけない。「重さ制限が 2」であり「品 2 の重さの余裕がある」ときの重さというのは、(品 2 の重さは 1 だから) 2 - 1 = 1 だ。重さ制限 1 のときなら、品 2 を追加することができる。
ここは自分が一番理解に苦労を要したところだったので、言い換えてもう一度書くぞ。重さ制限 1 のときの価値に品 2 の価値を足したものが、「品 2 を足されており」「重さ制限が 2 に収まる」両方の条件をクリアした価値だ。
現在のところ、品 1 まで選べて重さ制限 1 のときの最大価値は [1, 1] にある。 0 だ。そこに品 2 を加えたら、価値は 2 だ。
というわけで「品 1 まで選べる条件での最大価値と、品 2 を足した場合の価値の比較」は 3 と 2 の比較になる。 3 のほうが大きい。
だから品 2 まで選べて重さ制限 2 のときの最大価値は、(品 2 を足さないほうがマシで)3 のままということになる。

まとめると、この表のマスを埋めるときのロジックは次の通りになる。

マスを [i, w] とすると、 i 番目の品まで選べて重さ制限 w のときの最大価値がマスに入る。

- 品の重さは制限 w 以下か? 
    - NO: じゃあゼッテーその制限じゃ入れられねー。 -> ひとつ前の品での最大値 [i-1, w] が続投。
    - YES: 品が入る可能性があるな。続行↓
- ひとつ前の品での最大値 [i-1, w] と、品を足したときの価値 [i-1, w-品の重さ]+品の価値 と、どっちが大きい?
    - 前者: じゃあ続投。
    - 後者: じゃあ足したときの価値で更新。

このロジックで表を埋め続けると、こんな感じになるぞ。

	0	1	2	3	4	5	6
0	0	0	0	0	0	0	0
1	0	0	2	2	2	3	3
2	0	3	3	3	3	5	5
...
8	0	3	5	11	12	14	91
9	0	3	5	11	12	15	94

一番右下のマスが、品を 6 個全部考慮して、重さ制限 9 のときの最大価値だ。これがナップサック問題「なるべく『価値』の合計値がたくさんになるように品物を詰めろ!」の回答となる!

確か品物が 6 個のとき、全パターンを計算しようとしたら 63 通りを試さないといけなかったはずだ。でもこの表を使えば、(重さ制限 9 なら)54 個のマスを埋めるだけになっている。ちょっと減っている。もし品物が 25 個だったら、全パターンは 33554431 通りだ。この表を使えば、マスを 25 * 9 = 225 個埋めるだけだ。これは画期的じゃないか?

緑さんでも分かる解説終わり

これが、ぼくでも分かるナップサック問題の解説だ。いろいろネットの記事を見たけれど、ぼくの場合次の2点で理解が止まっちまった。

突然表が出てきて、表の意味がわからない。
「品 2 を足した場合の価値」は [i-1, w-品の重さ]+品の価値 だが、 w-品の重さ の部分がわからない。

その2点を自分なりにクリアできた方法を、記事にしたつもりだ。

練習編を踏まえることで、「表を左から埋めていけばいいんだな」と分かった。あといきなり x, y 表はハードルが高い。
品 n を足すときは、「品 n の重さぶんスペースのある状態に品 n を足すことで、制限 w を満たしかつ品 n を足した状態を実現できる」。

とくにふたつめがタイヘンだったので、そこは強調して書いたつもりだ。こちら↓がソコが分かった瞬間のノートである。

ほぎゃー! 分かった?! おしまい。

Omake

import itertools


def foo(item_amount: int) -> int:
    """品物が item_amount ぶんあるとき、選択数を含めた全組み合わせの数を計算する!"""

    # 品物リスト。
    lis = list(range(item_amount))
    x = 0
    # リストから i 個選ぶとき……
    for i in range(len(lis)):
        # 一体、何通り計算するハメになるのだ?
        for combination in itertools.combinations(lis, i):
            x += 1
    return x


# 品物が a 個あるとき、それぞれ組み合わせは何通りになっちまうんだ? 見てみようぜ。
for a in range(1, 26):
    print(f'{a}個あるとき……{foo(a)}')