緑さんでも分かるナップサック問題解説 Python 編

概要
動的計画法練習編を Python で
動的計画法本番を Python で
おしまい

概要

きのう書いたナップサック問題を Python で解こう!

(2020-12-07)緑さんでも分かるナップサック問題解説アルゴリズム編

確かにきのうの記事で、答えを出すための計算を 33554431 回から 225 回へ減らせたけれど、いや、それでも自分でやる気にはなれんわ! だから Python にやってもらおう。

動的計画法練習編を Python で

まずは練習のほう。「数値をいくつか用意したから、その中から好きなだけ数値を選んで、合計が最大になるものを出せ!」という問題だ。

たとえば [7, -6, 9] なら最大の組み合わせは 7, 9 で最大値は 16 だ。
たとえば [-9, -16] なら何も選ばないのが答えで、最大値は 0 だ。

解説は前の記事のここ(動的計画法練習編)。

def practice(lis: list) -> int:

    # 表を作ります。
    # 動的計画法を使うときの表は dp って名前にすることが多いみたいです。
    # いちばん左は「リストから 0 個選べるとき」の最大値です。もちろん 0。
    dp = [0]

    # 「リストから[リストの個数]選べるとき」の計算をするので、リストの個数ぶん回します。
    for i in range(len(lis)):

        # 「ひとつ前の値」と「今のところの最大値に lis[i] を足したもの」を比べます。
        # NOTE: dp[i] は「0 個選べるとき」のマスで、 lis[i] は「1 個目の要素」なのがちょっとわかりづらいトコ。
        dp.append(max(dp[i], dp[i] + lis[i]))

    print(dp)

    # for が終わると dp の最後の値が、全部の値を比べた結果の最大値になってるはずだ。
    return dp[-1]


print(practice([7, -6, 9]) == 16)

実行するとこう↓なる! OK!

[0, 7, 7, 16]
True

動的計画法本番を Python で

では本番だ。

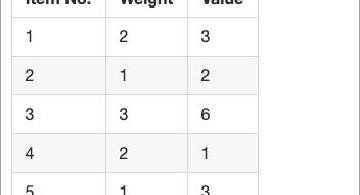
[(weight, value) = (2, 3), (1, 2), (3, 6), (2, 1), (1, 3), (5, 85)] というような品物リストと、重量制限 W が与えられる。
リストから、「weight 合計が W を超えないよう」「好きなだけ」品物を選んだときの value 最大値を出せ。

解説は前の記事のここ(動的計画法本番編)。

from pprint import pprint


def knapsack(lis: list, W: int) -> int:

    # 表を作ります。
    # dp[0] はリストから何も選んでないときの最大値じゃん? だから一番左の列は全部 0 です。
    dp = [[0] * (W + 1)]

    # リストの個数ぶん回します。
    for i in range(len(lis)):

        # i の周回では lis[i] までの品が選べるときの計算をします。
        weight = lis[i][0]
        value = lis[i][1]

        # lis[i] までの品が選べるときの情報を格納する配列です。もちろん [0]*W+1 です。
        dp.append([0] * (W + 1))

        # lis[i] までの品が選べる列のマスを埋めます。
        for w in range(W + 1):

            # lis[i] の重さが重量制限より上だったら、 lis[i] を追加することはできません。
            # この w 制限での value 最大値は、 lis[i] を追加する前の最大値(dp[i][w])と同じです。
            # NOTE: いま値を追加したいマスは、 dp[i][w] じゃなくて dp[i + 1][w] なのがちょっとわかりづらいトコ。
            if weight > w:
                dp[i + 1][w] = dp[i][w]
                continue

            # lis[i] を追加したときの最大値は、(ここがムズいんだが)
            # lis[i] を追加する前の最大値リストの中で、
            # lis[i] の入るスペースがあるときの最大値に lis[i] の価値を足したものです。
            _ = dp[i][w - weight] + value

            # lis[i] を足した場合の値と、 a[i] を足さなかったときの値(これまでの最大値)、大きいほうが、この条件下での最大値です。
            dp[i + 1][w] = max(_, dp[i][w])

    pprint(dp)

    # 一番はじっこ…… a の個数ぶん選べて、重量制限が W のときの最大値が、答えです。
    return dp[-1][-1]


print(knapsack([(2, 3), (1, 2), (3, 6), (2, 1), (1, 3), (5, 85)], 9) == 94)

実行するとこう↓なる! OK!

[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 0, 3, 3, 3, 3, 3, 3, 3, 3],
 [0, 2, 3, 5, 5, 5, 5, 5, 5, 5],
 [0, 2, 3, 6, 8, 9, 11, 11, 11, 11],
 [0, 2, 3, 6, 8, 9, 11, 11, 12, 12],
 [0, 3, 5, 6, 9, 11, 12, 14, 14, 15],
 [0, 3, 5, 6, 9, 85, 88, 90, 91, 94]]
True