Antonio Gulli and Sujit Pal『直感 Deep Learning』 ざっくり読み1章 ニューラルネットワークの基礎

概要

ぼくの大好きな Python は、機械学習の分野でけっこう有名だ。ぼくは全然興味ないので、親愛なるみろりHP読者諸兄が御存知の通り Python ではブログ作ったりプログラミング問題で遊んだりゲーム作ったりしている。

ただまあ。たしかに Python で機械学習は有名だ。 Pythonista の末席を汚すものとして、ちょっとは触ってみてもいいかもしれない。今回の読書の方針としては、

• 機械学習にまつわる用語、概念について「ああいうやつ」っていうイメージを持てるようにする
• それらについて『それ何?』って言われたときに自分の言葉で浅〜く答えられるようにする

てコトでざっくり読むよ。

1章をざっくり読んだ

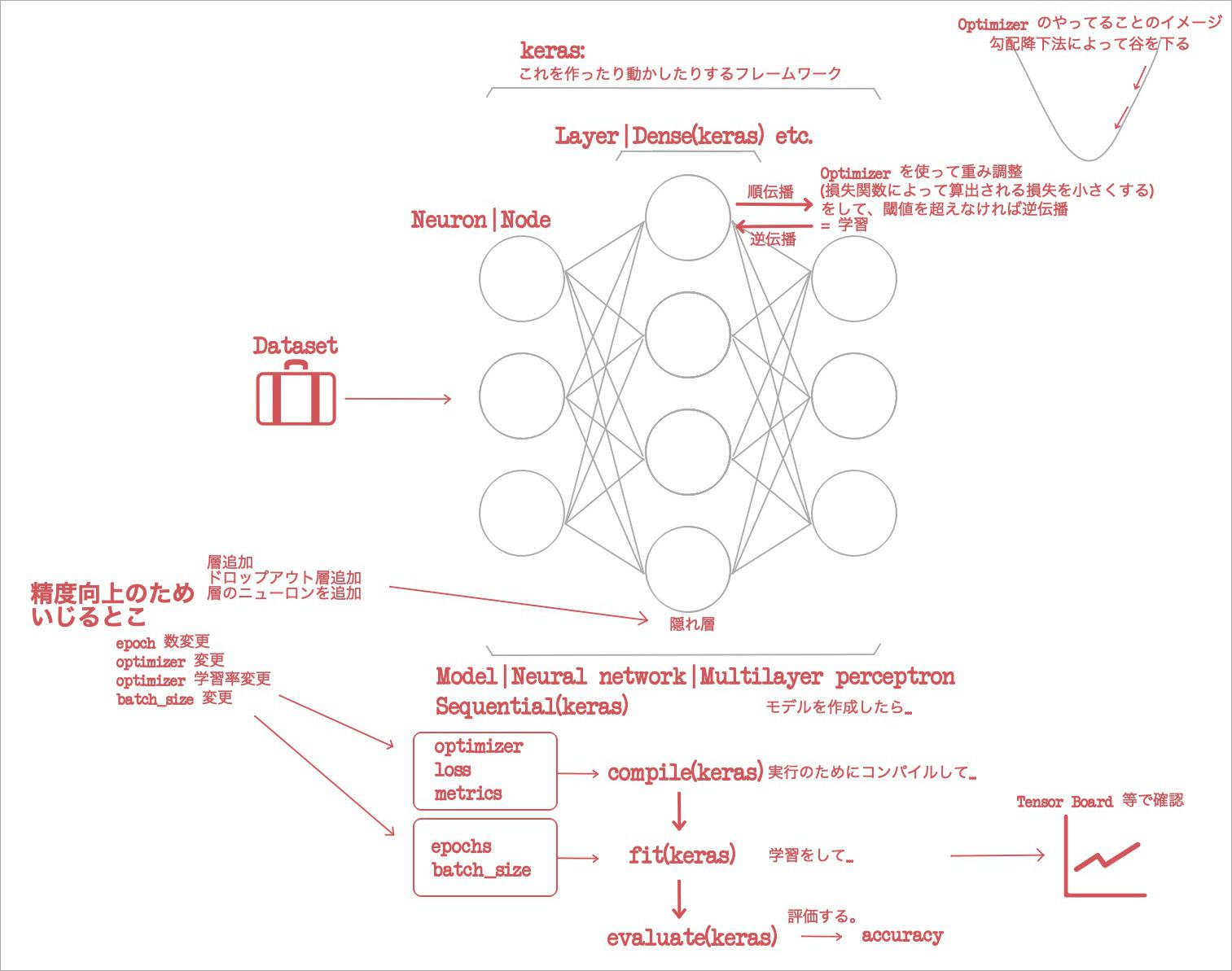
• Keras って何?
  • 学習コストが低いディープラーニングフレームワーク。
• ディープって何?
  • ディープに定義はない。むかしは10層でもディープだったけれど、現在は数百の層をディープとみなすのが一般的。
  • ディープラーニングは人間の視覚野が層になっていることからインスピレーションを得ている。人間の視覚は視覚皮質 V1 に接続されており、さらに V2, V3, V4, V5, V6 に接続され、複雑な画像処理を行う。
• パーセプトロンって何?
  • 0 or 1 だけ出力できる線形層をもつモデル。
  • 1章読み終わっても、結局パーセプトロンが層の中のノードを表すのか層そのものを表すのかはわからなかった。
  • 多層のネットワークを多層パーセプトロン(multilayer perceptron)という。
  • 1章読み終わっても、多層パーセプトロンとニューラルネットワークが同じなのかどうかわからなかった。
• 活性化関数って何?
  • シグモイド関数、 ReLU などの非線形関数のこと。
  • パーセプトロンの 0 or 1 じゃ漸次学習(次第に学ぶってこと)ができない。
  • だから 0 or 1 の線形関数でなくてを使わないと学習ができない。
  • 学習は、記憶よりも汎化が重要だからね。
  • パーセプトロンをつなげたところで結局 0 or 1 だから、活性化関数のニューロンをつなげれば緩やかな変化を出力できてまともな漸次学習ができるってわけね。
• 概念はいいとして Python で実際にネットワークを再現しようと思ったらどうやるの?
  • Keras のもっとも単純なモデルである Sequential を初期化して、層を .Add していくことで、ニューラルネットワークを作成する。
  • 「ニューラルネットワークを作成」と言ったけど、なんか「モデルを作成」って言い方がよくされているのでそっちでイメージをもっておく。
  • 今回の読書では Python コードはあんまり書かないでいく。ざっくりできなくなってドンドン長くなっていくから。理解の助けになるときだけちょっとだけ書くよ。
  • こちら↓層を追加している様子。

# 出力が12次元、入力が8次元の層 Dense を追加している。
# ニューロンを random_uniform ... -0.05 ~ 0.05 の範囲でランダムに初期化している。
# 他には random_normal とか zero とかある。
# これは初期化に使う重みを表す。 kernel って重みなんだ?
model.Add(Dense(12, input_dim=8, kernel_initializer='random_uniform'))

• MNIST dataset って何?
  • keras.datasets にデフォで含まれている手書き文字データセット。
  • データセットを探してくる手間ナシで、手書き文字の学習が遊べる。
• (ソースは書かないけど)ニューラルネットワークの作成、学習って Python でどんな流れでやるの?
  • データを学習データと評価データにわける。
  • それを one-hot encoding っていう手法で整理? する。
  • 層を追加する。層には Dense とか Activate とかある。層を追加し終わることをモデルを定義するという。
  • 実行のためにコンパイルをする。こちら↓コンパイルしている様子。コンパイルには次のようなオプションを与える。

model.compile(
    # オプションその1: 最適化アルゴリズム。
    optimizer=OPTIMIZER,
    # オプションその2: 損失関数。
    loss='categorical_crossentropy',
    # オプションその3: 評価関数。
    metrics=['accuracy']
)

• 最適化アルゴリズムって何?
  • ネットワークが学習される直感的イメージは「谷底を下る」である。
  • 勾配降下法によって、グラフ上における谷を下るという意味だ。
  • よくわかんないけれど、このイメージをとりあえずもっておく。底へいくほど良いのだ。
  • ほんで、その勾配降下法の種類として最適化アルゴリズムを指定するのだ。
  • SGD(stochastic gradient descent 確率的勾配降下法) とか RMSprop とか Adam とかある。
• 損失関数って内?
  • 最適化アルゴリズムが利用するもので、重み空間を最適な方向に導くために使われる……とあるがよくわからねえ。
  • MSE、バイナリクロスエントロピー、カテゴリカルクロスエントロピーとかある。
• 評価関数って何?
  • 学習には使われず、評価にだけ使われるやつ。
  • 精度、適合率、再現率、といった評価関数を使える。
• Tensor Board って何?
  • 学習データと検証データの精度を可視化できるライブラリ。
  • ああ、コンパイル↑のあとは学習に移るから、その精度をみるために用意するのね!
  • 「これやってるときにこれを意識する」っていうイメージの流れはぼくにとって大事。
• 学習って Python でどんな流れでやるの? のつづき。
  • fit 関数で学習を行う。学習には epochs batch_size といったパラメータを与える。
  • こんな↓感じだ。

model.fit(
    X_train,
    Y_train,
    batch_size=BATCH_SIZE,
    epochs=NB_EPOCH,
    verbose=VERBOSE,
    validation_split=VALIDATION_SPLIT,
)

• epochs って何?
  • モデルに何回データセットを学習させるか? という指定。
  • やりすぎると過学習になる。後述。
• batch_size って何?
  • 「最適化アルゴリズムが重みを更新するときにデータをいくつ使用するか」。
  • 何のデータだよ。機械学習の参考文章っていつも舌足らずだ。
• 上の過学習って何?
  • 「経験則として、損失が下がったあとに増加したら、それは過度に学習(epoch 増やしすぎ)しているってこと」。
  • 自分の言葉で言い換えると、「ああ、 epoch 数増やしていくときに、精度の上昇が止まって逆に下降することあるだろ。それだよ」
• 学習って Python でどんな流れでやるの? のつづきのつづき。
  • 最後に model.evaluate で score と accuracy を取得する。
  • accuracy に出ているのが90%だとしたら、10個のうち1個間違えるということ。
  • こんな↓感じだ。

score = model.evaluate(X_test, Y_test, verbose=VERBOSE)

• 誤差逆伝播法って何?
  • ネットワークにおいて値は通常、入力層->隠れ層->出力層へ値を順伝播する。
  • ただし学習時には正解がわかっているから、伝播したときに誤差があることが検知できる。
  • そのときそのまま順伝播せずに、逆伝播させる。そして誤差が所定の閾値より低くなるまで重みを調整する。このとき使われるのが最適化アルゴリズムだ。
  • そうやって多層パーセプトロンは学習をするのだ。

ここまで、「って何?」系の話をノートした。ここからは、出た accuracy を向上させる手順だ。

1. ネットワークに隠れ層を追加してみる。
   • model.add(Dense(N_HIDDEN) と model.add(Activation('(たとえば)softmax')) をいくつか繰り返し追加してみる、という意味だ。
   • これは一通りの方法ではなくて、良い結果を求めるためには、隠れ層の数を変えてみたり、しないといけないようだ。
2. ドロップアウト層を追加してみる。
   • model.add(Dropout(0.3)) を追加してみる、という意味だ。
   • 隠れ層にドロップアウトを使用すると、多くの場合汎化性能を向上できる。
   • 直感的にいうと、各ニューロンが近傍のニューロンに頼れなくなるので、より賢くなるということだ。
   • ドロップアウトの値を増やしすぎると精度が落ちていくようだ。
3. epoch 数を変えてみる。
   • 数値を変えて精度をグラフで見ることで、「これ以上訓練する必要ないな」と判断できたりするのだ。
4. 最適化アルゴリズムを変更してみる。
   • サンプルでは、 SGD から RMSprop や Adam に変えたら効果があったみたいだ。
   • 具体的には、少ない epoch 数でもはやく収束している。
   • 収束っていうのは、精度が上がりきるってことだね。
5. 最適化アルゴリズムの学習率を変えてみる。
   • あ? 学習率なんて言葉出てきたっけ?
6. 隠れ層のニューロンを増やしてみる。
   • 隠れ層自体を増やすのではなくて、そこに含まれるノードの数を増やすってことかな?
   • これを増やすとパラメータ数が増えて、学習に必要な時間が増加する。
7. バッチ計算サイズを変更してみる。
   • サンプルでは、増やしすぎるとがっくり精度が落ちているなあ。

こうやって精度を上げていくんだね。この微調整のプロセス……つまり最適なパラメータの組み合わせを探索するプロセスをハイパーパラメータチューニングという。その調整は勾配降下法のような最適化アルゴリズムを使って行う。

• 「学習データの精度は評価データの精度を超えるべき。超えない場合は学習回数を大幅に増やしてみましょう。」ここの例では epoch 数を20->250に増やすと精度が上がっている。
• n 個のパラメータがあるとすると、 n 次元空間を定義していることになる。ハイパーパラメータチューニングの目標は、この空間内からコスト関数を最適化する点を見つけること。
• んーー、まだ「コスト関数」がよくイメージできてないな。

こんなところで1章はおしまいだ。この本が推している、「直感的な理解」はぼくの方針とマッチしており、読みやすいと感じている。今回の読書については、「イメージの流れ」を図示できればよいかなと思う。だから図示してみた。