●
例によってプログラミング問題です。問題を見た瞬間おっもしろそー! と思った。
# これを…… -> こうする!
# ######## #+########
# ## ### # #+## ### #
# ## # #++++## #
#### ## ####+ ##
# ## ##### -> # ##+#####
# # # #++++#+++#
# #### # # #+####+#+#
# # # #++++++#+#
## ## ## # ## ## ##+#
######## # ########+#
●
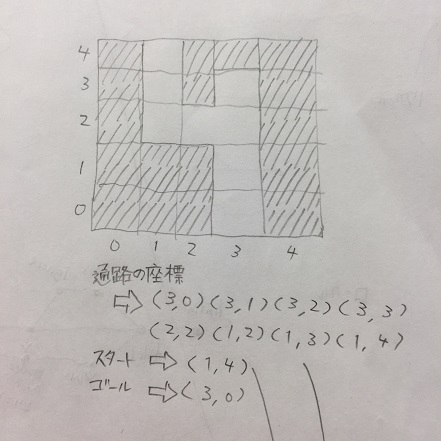
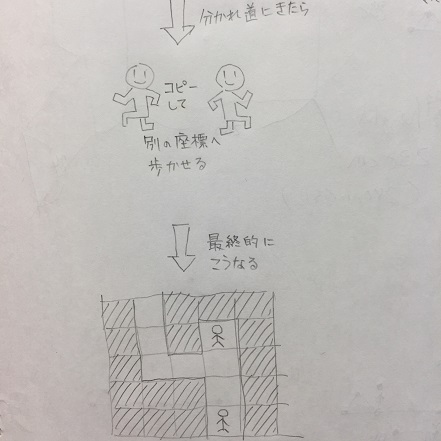
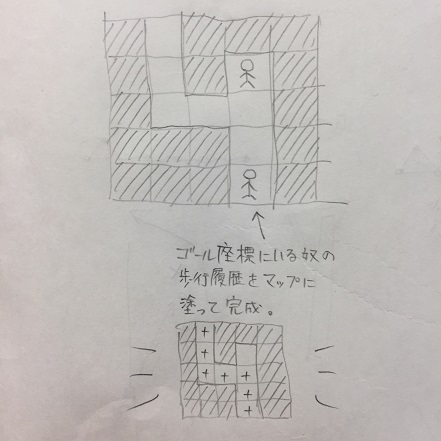
みどりんの考えたのがこういうロジック。

●
メインロジック。いちばん上の solve_maze がトップレベル。
import os, itertools, copy, enum
def solve_maze(maze):
"""迷路を解きます。"""
# 最初の奴隷を用意します。
first_walker = Walker()
# 通路座標を奴隷の歩行可能座標として登録します。
first_walker.walkable_points = maze.pathways
# こいつをスタート地点に立たせます。
first_walker.start_point = maze.start_point
first_walker.step_to(maze.start_point)
# 分かれ道のたびに、奴隷を増殖させて袋小路まで進ませます。
# そのたびにwalkersリストに追加されるので、最終的に全通りのルートがwalkersに登録されることになります。
walkers = [first_walker]
for walker in walkers:
# 奴隷ひとりにつき再帰関数ひとめぐり。
walker_life(walker, walkers)
# 勝者を決めます。
winner = compete_walkers(walkers, maze)
return winner
def walker_life(walker, walkers):
"""奴隷の歩みを処理する再帰関数です。"""
# 今いるマスの東西南北に道があるか調べます(一度踏んだマスは通れない)。
next_points = walker.look_around_next_points()
# 進める場所がない場合、そいつは終了です。
if not next_points:
return
# 道がひとつだけある場合、次のマスへ移動させます。
if len(next_points) == 1:
walker.step_to(next_points[0])
# 道が2以上ある場合、奴隷を分裂させます。
else:
process_for_multiple_possibilities(walker, next_points, walkers)
walker_life(walker, walkers)
def process_for_multiple_possibilities(walker, next_points, walkers):
"""道が2以上ある場合の処理です。forが長くなるのヤだから分離しました。"""
# 進む前の奴隷をコピーしておきます。
walker_copies = [walker.create_myself() for i in range(len(next_points) - 1)]
# 現奴隷は次のマスへ移動します。
walker.step_to(next_points[0])
next_points.pop(0)
# コピーした奴隷たちを、それぞれ別の分かれ道へ進ませます。
# そして次の while のためwalkersリストに溜めておきます。
for walker_copy, next_point in zip(walker_copies, next_points):
walker_copy.step_to(next_point)
walkers.append(walker_copy)
def compete_walkers(walkers, maze):
"""最優秀ゴール者を決めます。関数が長くなるのヤだから分離しました。"""
# 奴隷の中から、ゴールした連中を取り出します。
goal_walkers = list(filter(lambda walker: walker.stand_point == maze.goal_point, walkers))
# インデックスとwalker.step_numのディクショナリ。{0:30, 1:25, 2:10}みたいになる。
dic = {i: goal_walker.step_num for i, goal_walker in enumerate(goal_walkers)}
# step_numでの昇順ソート。[(2,10), (1,25), (0,30)]みたいになる。
ranking = sorted(dic.items(), key=lambda value: value[1])
# ゴール者の中で、最短距離をいった者が最優秀ゴール者です。
return goal_walkers[ranking[0][0]]
迷路のマスを定義する。ぶっちゃけ今回のプログラムではあんまり必要ないクラスだけど enum っていうのを使ってみたくてさあ。
class MazeSigns(enum.Enum):
""" 迷路のマスをenumで定義してみます。
具体値の取り出し方は MazeSigns.WALL.value こう。"""
WALL = '#'
PATHWAY = ' '
FOOTPRINT = '+'
STAND_POINT = '*'
迷路データを簡単に扱えるようにするクラス。ちょっと色気づいて、最近オライリーで覚えた private 属性を使ってみた。
class Maze:
""" 迷路データを簡単に扱うためのクラス!
ほら、文字列のままだと座標指定でマスを取得するとかできないじゃん?
そういうのができるようになります。10x10だけに対応してるよ!"""
def __init__(self, original_maze):
self.original_maze = original_maze
# MazeSignsのディクショナリ。
self.sign_dic = {sign.value:sign for sign in MazeSigns}
# マップ文字列を二次元配列にしたものです。
self.map_list = self.__convert_map_to_list()
# 通路部分の座標のリストです。
self.pathways = self.__make_pathways()
# この迷路のスタート地点とゴール地点です。
_ = self.__get_entrances()
self.start_point = _[0]
self.goal_point = _[1]
def __convert_map_to_list(self):
"""(private)マップ文字列を二次元配列にして、中身を全部MazeSigns型に変換します。"""
lines = list(filter(lambda line: line != '', self.original_maze.split(os.linesep)))
lines.reverse()
# マネしちゃダメな堂々の二重内包表記。クソ読みづらい(笑)
return [[self.sign_dic[cell] for cell in list(line)] for line in lines]
def __make_pathways(self):
"""(private)歩行可能座標のリストを作ります。"""
# 通路の部分の座標を求めます。
pathways = []
for x, y in itertools.product(range(10), range(10)):
if self.map_list[y][x] == MazeSigns.PATHWAY:
pathways.append((x, y))
return pathways
def __get_entrances(self):
"""(private)迷路のスタート地点とゴール地点を求めます。"""
entrances = []
for coordinate in self.pathways:
if coordinate[0] in [0, 9] or coordinate[1] in [0, 9]:
entrances.append(coordinate)
return entrances
迷路を歩かせる奴隷を作成するクラス。
class Walker:
"""迷路を歩く奴隷を意味するクラス! 自分が歩いた座標を記録していくよ!"""
# インスタンスひとつひとつに振るIDです。
walker_id = 0
def __init__(self):
# ID。
self.walker_id = Walker.walker_id
# 初期座標。
self.start_point = None
# 現在地。
self.stand_point = None
# 歩行可能座標。
self.walkable_points = []
# 歩行履歴。
self.walk_history = []
# 歩行数。
self.step_num = 0
def __str__(self):
"""str(walker)したとき現在のコイツの状態を返します。"""
return os.linesep.join([
f'',
f'初期座標:{self.start_point}',
f'現在地:{self.stand_point}',
f'残歩行可能座標:{self.walkable_points}',
f'歩行履歴:{self.walk_history}',
f'歩行数:{self.step_num}',
])
def step_to(self, next_point):
"""引数の座標へ歩みます。"""
self.stand_point = next_point
self.walk_history.append(next_point)
self.walkable_points.remove(next_point)
self.step_num += 1
def look_around_next_points(self):
"""今のマスの東西南北に歩行可能マスがあるか調べます。"""
# 東西南北の座標です。
next_points = [
(self.stand_point[0], self.stand_point[1]+1),
(self.stand_point[0], self.stand_point[1]-1),
(self.stand_point[0]+1, self.stand_point[1]),
(self.stand_point[0]-1, self.stand_point[1]),
]
# 進める座標は、歩行履歴になくて歩行可能座標にあるもの。
next_points = filter(lambda point: point not in self.walk_history, next_points)
next_points = filter(lambda point: point in self.walkable_points, next_points)
return list(next_points)
def create_myself(self):
"""自分自身のコピーを作ります。"""
walker = copy.deepcopy(self)
walker.walker_id += 1
return walker
def draw_steps_on_map(self, maze):
"""自分が歩いた軌跡をマップに書きます。"""
map_list = maze.map_list
for coordinate in self.walk_history:
map_list[coordinate[1]][coordinate[0]] = (
MazeSigns.STAND_POINT if coordinate == self.stand_point else MazeSigns.FOOTPRINT)
# 文字列にします。マネしちゃダメな堂々の 3重 内包表記。クッソ読みづらい。
map_list.reverse()
return os.linesep.join([''.join(m) for m in [[maze_sign.value for maze_sign in line] for line in map_list]])
実行はこんな感じ。
#####################################################################
# ここまでプログラム。ここから実施。
#####################################################################
questions = [
'''
##########
##########
##########
###
### ####
### ####
### ####
### ####
####
##########
''',
'''
##########
### #
### ## # #
### ## # #
# ##
# # #### #
# # #
# ########
# ####
##### ####
''',
]
for i, question in enumerate(questions):
maze = Maze(question)
winner = solve_maze(maze)
print()
print(f'-*-*-*-* question{i} *-*-*-*-')
print(winner)
print(winner.draw_steps_on_map(maze))
結果はこう!
-*-*-*-* question0 *-*-*-*-
<Walker オブジェクト ID:2>
初期座標:(0, 1)
現在地:(9, 6)
残歩行可能座標:[(3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 2), (4, 3), (4, 4), (4, 5), (4, 6)]
歩行履歴:[(0, 1), (1, 1), (2, 1), (3, 1), (4, 1), (5, 1),
(5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 6),
(7, 6), (8, 6), (9, 6)]
歩行数:15
##########
##########
##########
### ++++*
### +####
### +####
### +####
### +####
++++++####
##########
-*-*-*-* question1 *-*-*-*-
<Walker オブジェクト ID:2>
初期座標:(5, 0)
現在地:(9, 5)
残歩行可能座標:[(3, 6), (3, 7), (3, 8), (4, 8), (5, 8),
(6, 5), (6, 6), (6, 7), (6, 8), (7, 5),
(7, 8), (8, 6), (8, 7), (8, 8)]
歩行履歴:[(5, 0), (5, 1), (4, 1), (3, 1), (2, 1),
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5),
(2, 5), (3, 5), (3, 4), (3, 3), (4, 3),
(5, 3), (6, 3), (7, 3), (8, 3), (8, 4),
(8, 5), (9, 5)]
歩行数:22
##########
### #
### ## # #
### ## # #
#+++## +*
#+#+####+#
#+#++++++#
#+########
#+++++####
#####+####
●
迷路を解くだけでなく、最短距離を求められてる。完璧! クラスを効果的に使えてるし、内包表記や高階関数を使いすぎなまでに使ってるし、再帰関数も使えてる。満足!